Leetcode 104: Maximum Depth of Binary Tree

Problem

Leetcode 104 - Maximum Depth of Binary Tree

Example:

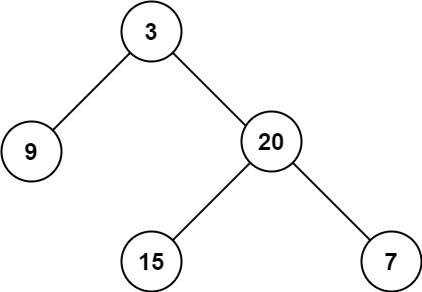
Input: root = [3,9,20,null,null,15,7]
Output: 3

Approach

This problem can be solved using a recursive approach. First, we check if the root is None, if so, we return 0 as the depth of the tree should be 0 of no root. Then, we recursively call the function on the left and right subtree of the root, and return the maximum depth between the left and right subtree plus 1 (for the root).

Visualization of the approach:

root: 3
    3
   / \
  9  20
     / \
    15  7

Since root is not None, we recursively call the function on the left and right subtree of the root.

root: 9
    9
   / \

Since root is not None, we recursively call the function on the left and right subtree of the root.

root: None

Since root is None, we return 0. Thus, the root 9 has a depth of 1.

root: 20
    20
   / \
  15  7

Since root is not None, we recursively call the function on the left and right subtree of the root.

root: 15
    15
   / \  

Since root is None, we return 0. Thus, the root 15 has a depth of 1.

root: 7
    7
   / \

Since root is None, we return 0. Thus, the root 7 has a depth of 1.

Finally, we return the maximum depth between the left and right subtree of the root plus 1, which is 2.

root: 3
    3
   / \
  9  20
     / \
    15  7   

The maximum depth of the binary tree is 3, as the root 9 has a depth of 1, the root 20 has a depth of 2, thus the root 3 has a depth of max(1, 2) + 1 = 3.

Here is the implementation of the approach:

class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        # Base case: if the root is None, return 0
        if not root:
            return 0
        # Recursively call the function on the left and right subtree of the root
        return max(self.maxDepth(root.left), self.maxDepth(root.right)) + 1

Time Complexity and Space Complexity

Time Complexity: $O(n)$, where $n$ is the number of nodes in the tree. This is because we need to visit each node in the tree exactly once.

Space Complexity: $O(h)$, where $h$ is the height of the tree. This is because we need to store the call stack for the recursive function calls.