Leetcode 124. Binary Tree Maximum Path Sum
Explanation for Leetcode 124 - Binary Tree Maximum Path Sum, and its solution in Python.
Problem
Leetcode 124 - Binary Tree Maximum Path Sum
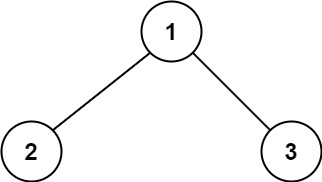
1
2
3
Input: root = [1,2,3]
Output: 6
Explanation: The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.
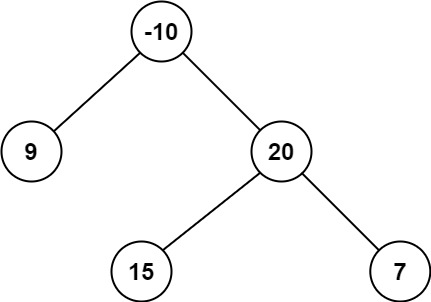
1
2
3
Input: root = [-10,9,20,null,null,15,7]
Output: 42
Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.
Approach
We can use DFS to solve this problem, with it we can track maxPath, and maxValue.
maxValue of the root would be root.val + maxPath of left + maxPath of right.
There are some cases that we need to consider for updating path:
- maxPath from left + root.val
- maxPath from right + root.val
- root.val (in case maxPath from left and right are negative, and root.val is non negative)
- 0 (in case maxPath + root.val is negative)
There are some cases that we need to consider for updating maxVal:
- maxPath from left + maxPath from right + root.val
- maxValue from left
- maxValue from right
- root.val (if others are all negative)
We can track of maxPath and maxVal as a base case.
Here is the Python code for the solution:
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution:
def maxPathSum(self, root: Optional[TreeNode]) -> int:
if not root:
return [0, float('-inf')]
left = root.left
right = root.right
path = max(left[0]+root.val, right[0]+root.val, root.val, 0)
maxVal = max(left[0]+right[0]+root.val, left[1], right[1], root.val)
return [path, maxVal]
return dfs(root)[1]
Time Complexity and Space Complexity
Time Complexity: $O(n)$
Space Complexity: $O(n)$
This post is licensed under CC BY 4.0 by the author.