Leetcode 337. House Robber III

Problem

Leetcode 337 - House Robber III

Example:

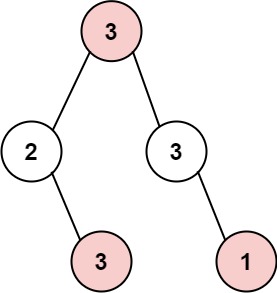
Input: root = [3,2,3,null,3,null,1]
Output: 7
Explanation: Maximum amount of money the thief can rob = 3 + 3 + 1 = 7.

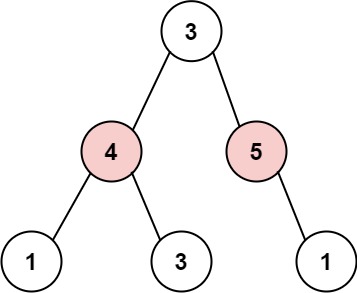
Input: root = [3,4,5,1,3,null,1]
Output: 9
Explanation: Maximum amount of money the thief can rob = 4 + 5 = 9.

Approach

There are 2 cases to calculate the maximum value for following tree or subtree:

• With Root: total value of the tree including the root value
• Without Root: total value of the tree without the root value

If we have no TreeNode, then it would result it [0, 0].

More clarification is shown in the Visualization below

Visualization of the Approach:

Input:
                3
            /       \
        2               3
          \               \
            3               1    

We can use dfs to calculate the deepest node first.

node: None
res = [0,0]
With root = 0 as there's no root value
Without root = 0 as there's no child

node: 3
res = [3, 0]
With root = 3 as root value + root.left's without root + root.right's without root = 3 + 0 + 0
Without root = 0 as there's no child

node: 2
res = [2, 3]
With root = 2 as root value + root.left's without root + root.right's without root = 2 + 0 + 0
Without root = 3 as max(root.left) + max(root.right) = 0 + 3

node: None
res = [0, 0]
With root = 0 as there's no root value
Without root = 0 as there's no child

node: 1 
res = [1, 0]
With root = 1 as root value + root.left's without root + root.right's without root = 1 + 0 + 0
Withotu rot = 0 as there's no child

node: 3
res = [3, 1]
With root = 3 as root value + root.left's without root + root.right's without root = 3 + 0 + 0
Without root = 1 as max(root.left) + max(root.right) = 0 + 1

node: 3
res = [7, 6]
With root = 7 as root value + root.left's without root + root.right's without root = 3 + 3 + 1 
Without root = 6 as max(root.left) + max(root.right) = 3 + 3

Thus return 7

Here is the Python code for the solution:

class Solution:
    def rob(self, root: Optional[TreeNode]) -> int:
        def dfs(root):
            if not root:
                return [0, 0]
            
            left = dfs(root.left)
            right = dfs(root.right)
            return [root.val + left[1] + right[1], max(left) + max(right)]
        
        return max(dfs(root))    

Time Complexity and Space Complexity

Time Complexity: $O(n)$

Space Complexity: $O(n)$