Leetcode 427. Construct Quad Tree

Problem

Leetcode 427 - Construct Quad Tree

Example:

Input: grid = [[0,1],[1,0]]
Output: [[0,1],[1,0],[1,1],[1,1],[1,0]]
Explanation: The explanation of this example is shown above:
Notice that 0 represents False and 1 represents True in the photo representing the Quad-Tree.

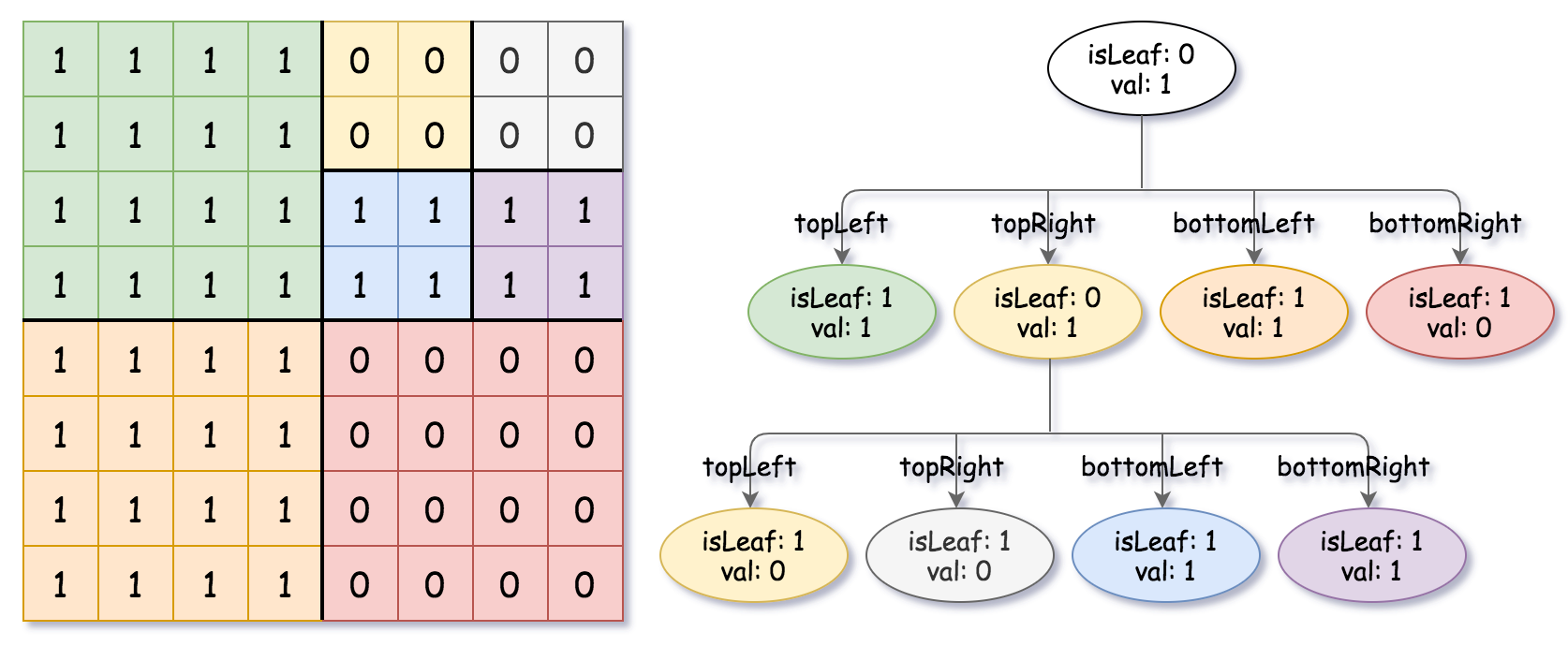
Input: grid = [[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0],[1,1,1,1,1,1,1,1],[1,1,1,1,1,1,1,1],[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0]]
Output: [[0,1],[1,1],[0,1],[1,1],[1,0],null,null,null,null,[1,0],[1,0],[1,1],[1,1]]
Explanation: All values in the grid are not the same. We divide the grid into four sub-grids.
The topLeft, bottomLeft and bottomRight each has the same value.
The topRight have different values so we divide it into 4 sub-grids where each has the same value.
Explanation is shown in the photo above:

Approach

Have a DFS helper function that takes in parameter $n$, $row$, and $col$. $n$ is the size of the current square grid section, and we will divide it by 2 to get the mid point. $row$ represents the starting row index of the current section. $col$ represents the starting col index of the current section.

Base case:

• if n == 1, we return Node(grid[row][col] == 1, true)

Using this information we can get

• topLeft = dfs(mid, row, col)
• topRight = dfs(mid, row, col+mid)
• bottomLeft = dfs(mid, row+mid, col)
• bottomRight = dfs(mid, row+mid, col+mid)

After processing all four quadrant, we check if they can be merged by checking

• if all quadrant are leaves and have the same value
• create a new leaf node with common value

Here is the Python code for the solution:

class Solution:
    def construct(self, grid: List[List[int]]) -> 'Node':
        def dfs(n, row, col):
            if n == 1:
                return Node(gird[row][col] == 1, True)
            
            mid = n//2
            topLeft = dfs(mid, row, col)
            topRight = dfs(mid, row, col+mid)
            bottomLeft = dfs(mid, row+mid, col)
            bottomRight = dfs(mid, row+mid, col+mid)

            if (topLeft.isLeaf and topRight.isLeaf and bottomLeft.isLeaf and bottomRight.isLeaf and
                topLeft.val == topRight.val == bottomLeft.val == bottomRight.val):
                return Node(topLeft.val, True)
            
            return Node(False, False, topLeft, topRight, bottomLeft, bottomRight)
        
        return dfs(len(grid), 0, 0)
    

Time Complexity and Space Complexity

Time Complexity: $O(n^2)$

Space Complexity: $O(log n)$