Leetcode 450. Delete Node in a BST
Explanation for Leetcode 450 - Delete Node in a BST, and its solution in Python.
Problem
Leetcode 450 - Delete Node in a BST
Example:
1
2
3
4
5
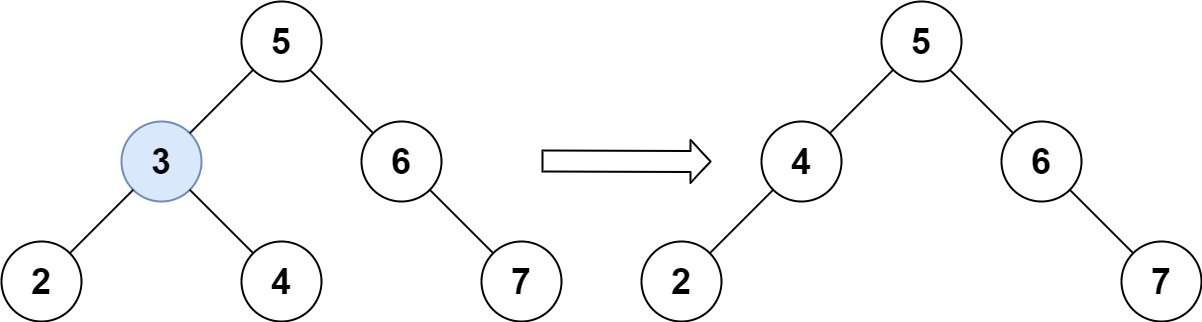
Input: root = [5,3,6,2,4,null,7], key = 3
Output: [5,4,6,2,null,null,7]
Explanation: Given key to delete is 3. So we find the node with value 3 and delete it.
One valid answer is [5,4,6,2,null,null,7], shown in the above BST.
Please notice that another valid answer is [5,2,6,null,4,null,7] and it's also accepted.
1
2
3
Input: root = [5,3,6,2,4,null,7], key = 0
Output: [5,3,6,2,4,null,7]
Explanation: The tree does not contain a node with value = 0.
Approach
Here is the Python code for the solution:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
class Solution:
def deleteNode(self, root: Optional[TreeNode], key: int) -> Optional[TreeNode]:
# if there is no root
if not root:
return root
parent = None
curr = root
# find the TreeNode to delete
while curr and curr.val != key:
parent = curr
if key > curr.val:
curr = curr.right
else:
curr = curr.left
# if the target doesn't work, return the Tree
if not curr:
return root
# if there's no child or 1 child of curr
if not curr.left or not curr.right:
child = curr.left if curr.left else curr.right
if not parent:
return child
# if parent's left is the current make the child to curr
if parent.left == curr:
parent.left = child
# if parent's right is the current, make the child to curr
else:
parent.right = child
# if there are 2 childs for curr
else:
par = None
delNode = curr
# since right has to be our new curr, go to curr.right
curr = curr.right
# get the left most child, and its parent
while curr.left:
par = curr
curr = curr.left
# if child's parent exists move all the right child to parent's left
if par:
par.left = curr.right
curr.right = delNode.right
# connect child's left to delNode's left
curr.left = delNode.left
# if child's parent doesn't exist
if not parent:
return curr
# if parent'left is delNode
if parent.left == delNode:
parent.left = curr
else:
parent.right = curr
return root
Time Complexity and Space Complexity
Time Complexity: $O(h)$ where $h$ is height of the tree
Space Complexity: $O(1)$
This post is licensed under CC BY 4.0 by the author.