Leetcode 543: Diameter of Binary Tree
Explanation for Leetcode 543 - Diameter of Binary Tree problem, and its solution in Python.
Problem
Leetcode 543 - Diameter of Binary Tree
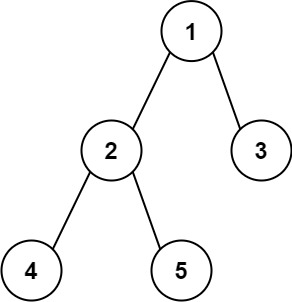
Example:
1
2
Input: root = [1,2,3,4,5]
Output: 3
Approach
Non-optimized solution
This problem can be solved using Leetcode 104 - Maximum Depth of Binary Tree problem as a helper function. Since the diameter of a binary tree is defined as the length of the longest path between any two nodes in the tree, it is the sum of the depth of the left subtree and the depth of the right subtree.
Thus, we can call the helper function on the left and right subtree of the root, and calculate the diameter of the binary tree that contains the root. However, we also need to consider the diameter that does not contain the root, which is the sum of the depth of the left subtree and the depth of the right subtree of the root’s left and right child respectively which we can call it subdiameter.
Therefore, the diameter of the binary tree is the maximum of the diameter that contains the root and the diameter that does not contain the root (subdiameter). However, this approach is not efficient because it requires us to calculate the diameter of the binary tree twice for each node.
Optimized solution
To optimize the solution, we can use depth first search to calculate the diameter of the binary tree. Meaning, we can calculate the diameter of the left and right subtree recursively and store the result in a dictionary.
Visualization of the approach:
Unoptimized solution
1
2
3
4
5
6
7
8
9
10
11
1
/ \
2 3
/ \
4 5
4: diameter = 0 since it has no children
5: diameter = 0 since it has no children
2: diameter = 2 since max(diameter of 4, diameter of 5) = max(0, 0) = 0, diameter = maxdepth(4) + maxdepth(5) = 1 + 1 = 2
3: diameter = 0 since it has no children
1: diameter = 3 since max(diameter of 2, diameter of 3) = max(2, 0) = 2, diameter = maxdepth(2) + maxdepth(3) = 2 + 1 = 3
Optimized solution
1
2
3
4
5
6
7
8
9
10
11
1
/ \
2 3
/ \
4 5
4: left = 0, right = 0, diameter = left + right = 0 + 0 = 0
5: left = 0, right = 0, diameter = left + right = 0 + 0 = 0
2: left = 1, right = 1, diameter = left + right = 1 + 1 = 2 update diameter to 2 since it is greater than the previous diameter
3: left = 0, right = 0, diameter = left + right = 0 + 0 = 0
1: left = 2, right = 1, diameter = left + right = 2 + 1 = 3 update diameter to 3 since it is greater than the previous diameter
Here is the implementation of the approach:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
### Non-optimized solution
class Solution:
def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:
# Base case: if the root is None, the diameter is 0
if not root:
return 0
# Calculate the diameter of tree including the root (max depth of left + max depth of right)
left = self.maxDepth(root.left)
right = self.maxDepth(root.right)
diameter = left + right
# Maximum diameter of subtree (left and right)
subdiameter = max(self.diameterOfBinaryTree(root.left), self.diameterOfBinaryTree(root.right))
# Return the maximum of the diameter that contains the root and the diameter that does not contain the root
return max(diameter, subdiameter)
# Helper function to calculate the maximum depth of a binary tree
def maxDepth(root):
if not root:
return 0
return 1 + max(maxDepth(root.left), maxDepth(root.right))
### Optimized solution
class Solution2:
def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:
# Initialize the diameter to 0
diameter = 0
# Define a helper function(dfs) to calculate the diameter of the binary tree
def dfs(root):
# Base case: if the root is None, return 0
if not root:
return 0
# Recursively call the function on the left and right subtree of the root
left = dfs(root.left)
right = dfs(root.right)
# Update the diameter if the current diameter is greater than the previous diameter
diameter = max(diameter, left + right)
# Return the maximum depth of the left and right subtree
return 1 + max(left, right)
# Call the helper function on the root
dfs(root)
return diameter
Time Complexity and Space Complexity
Time Complexity: $O(n)$, where $n$ is the number of nodes in the tree. This is because we need to visit each node in the tree exactly once.
Space Complexity: $O(h)$, where $h$ is the height of the tree. This is because we need to store the call stack for the recursive function calls.