Leetcode 84. Largest Rectangle in Histogram

Problem

Leetcode 84 - Largest Rectangle in Histogram

Example:

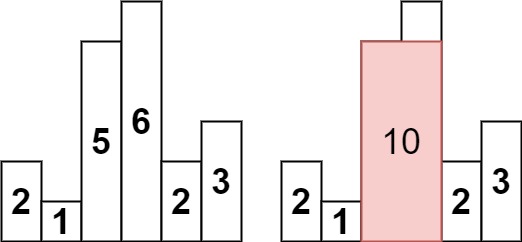
Input: heights = [2,1,5,6,2,3]
Output: 10
Explanation: The above is a histogram where width of each bar is 1.
The largest rectangle is shown in the red area, which has an area = 10 units.

Input: heights = [2,4]
Output: 4

Approach

Visualization of the Approach:

heights = [2,1,5,6,2,3]

stack = []
maxArea = 0

stack = [(0,2)]

stack[-1][1] > h, thus update maxArea and pop stack
maxArea = 2

stack = [(1,1)]

stack = [(1,1), (2,5)]

stack = [(1,1), (2,5), (3,6)]

stack[-1][1] > h, thus update maxArea and pop stack
maxArea = max(2, 6) = 6

stack[-1][1] > h, thus update maxArea and pop stack
maxArea = max(6, 10) = 10

stack = [(1,1), (4,2)]

stack = [(1,1), (4,2), (5,3)]

Since we've went to all loop, we must go through stack

stack = [(4,2), (5,3)]
maxArea = max(10, 5) = 10

stack = [(5,3)]
maxArea = max(10, 8) = 10

stack = []
maxArea = max(10, 3) = 10

return maxArea = 10

Here is the Python code for the solution:

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        stack = []
        maxArea = 0

        for i, h in enumerate(heights):
            start = i
            while stack and stack[-1][1] > h:
                stackI, stackH = stack.pop()
                maxArea = max(maxArea, stackH * (i-stackI))
                start = stackI
            stack.append((start, h))
        
        for i, h in stack:
            maxArea = max(maxArea, h * (len(heights)-1))
        
        return maxArea    

Time Complexity and Space Complexity

Time Complexity: $O(n)$

Space Complexity: $O(n)$