Leetcode 994. Rotting Oranges

Problem

Leetcode 994 - Rotting Oranges

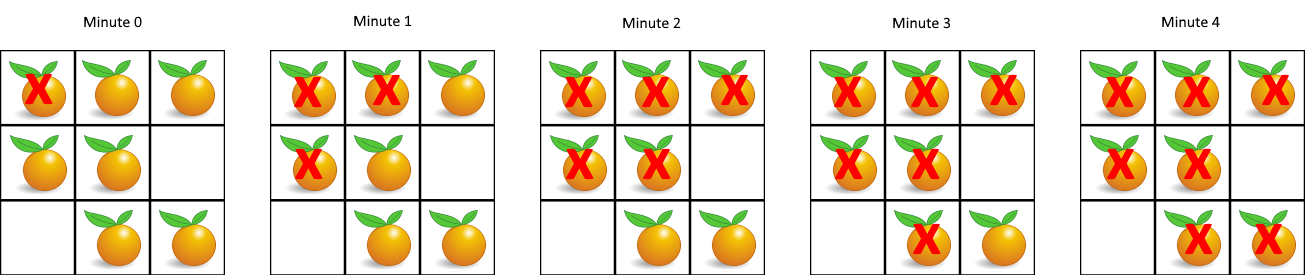
Example:

Input: grid = [[2,1,1],[1,1,0],[0,1,1]]
Output: 4

Input: grid = [[2,1,1],[0,1,1],[1,0,1]]
Output: -1
Explanation: The orange in the bottom left corner (row 2, column 0) is never rotten, because rotting only happens 4-directionally.

Input: grid = [[0,2]]
Output: 0
Explanation: Since there are already no fresh oranges at minute 0, the answer is just 0.

Approach

We can use BFS to find the the fresh oranges and increment time as oranges rot

After we can check if there still exists fresh orange and if it does, we return -1 else we return res

Here is the Python code for the solution:

class Solution:
    def orangesRotting(self, grid: List[List[int]]) -> int:
        res = 0
        q = deque()

        for i in range(len(grid)):
            for j in range(len(grid[0])):
                if grid[i][j] == 2:
                    q.append((i,j))

        while q:
            for i in range(len(q)):
                curr = q.popleft()
                if (curr[0]+1 < len(grid) and grid[curr[0]+1][curr[1]] == 1):
                    grid[curr[0]+1][curr[1]] = 2
                    q.append((curr[0]+1, curr[1])) 
                if curr[0]-1 >= 0 and grid[curr[0]-1][curr[1]] == 1:
                    grid[curr[0]-1][curr[1]] = 2
                    q.append((curr[0]-1, curr[1])) 
                if curr[1]+1 < len(grid[0]) and grid[curr[0]][curr[1]+1] == 1:
                    grid[curr[0]][curr[1]+1] = 2
                    q.append((curr[0], curr[1]+1)) 
                if curr[1]-1 >= 0 and grid[curr[0]][curr[1]-1] == 1:
                    grid[curr[0]][curr[1]-1] = 2
                    q.append((curr[0], curr[1]-1)) 
            res += 1 if q else 0
        
        for i in range(len(grid)):
            for j in range(len(grid[0])):
                if grid[i][j] == 1:
                    return -1
        
        return res

Time Complexity and Space Complexity

Time Complexity: $O(n * m)$

Space Complexity: $O(n * m)$